Implement the Self-Attention Mechanism in PyTorch
Python implementation of the self (scaled-dot product) attention mechanism originally proposed in “Attention Is All You Need”. Note that this is intended to be an executable and extended version of this article.
Would you like to download the code? Check out this GitHub repository.
Setup
import torch
import torch.nn.functional as F
torch.manual_seed(42)
dim_word_embedding = 16
Let’s map each unique word present in the sentence to an index. In real-world scenarios, there would be a bigger vocubalary, e.g. hundred of thousands of words.
sentence = 'Life is short, eat dessert first is life'
sentence = sentence.lower().replace(',', '').split()
n_sentence = len(sentence)
dict_words = {word: idx for idx, word in enumerate(sorted(sentence))}
sentence_ints = torch.tensor([dict_words[char] for char in sentence])
print('Word dictionary =', dict_words)
print('Numeric representation of the input sentence =', sentence_ints)
Word dictionary = {'dessert': 0, 'eat': 1, 'first': 2, 'is': 4, 'life': 6, 'short': 7}
Numeric representation of the input sentence = tensor([6, 4, 7, 1, 0, 2, 4, 6])
Single head self-attention
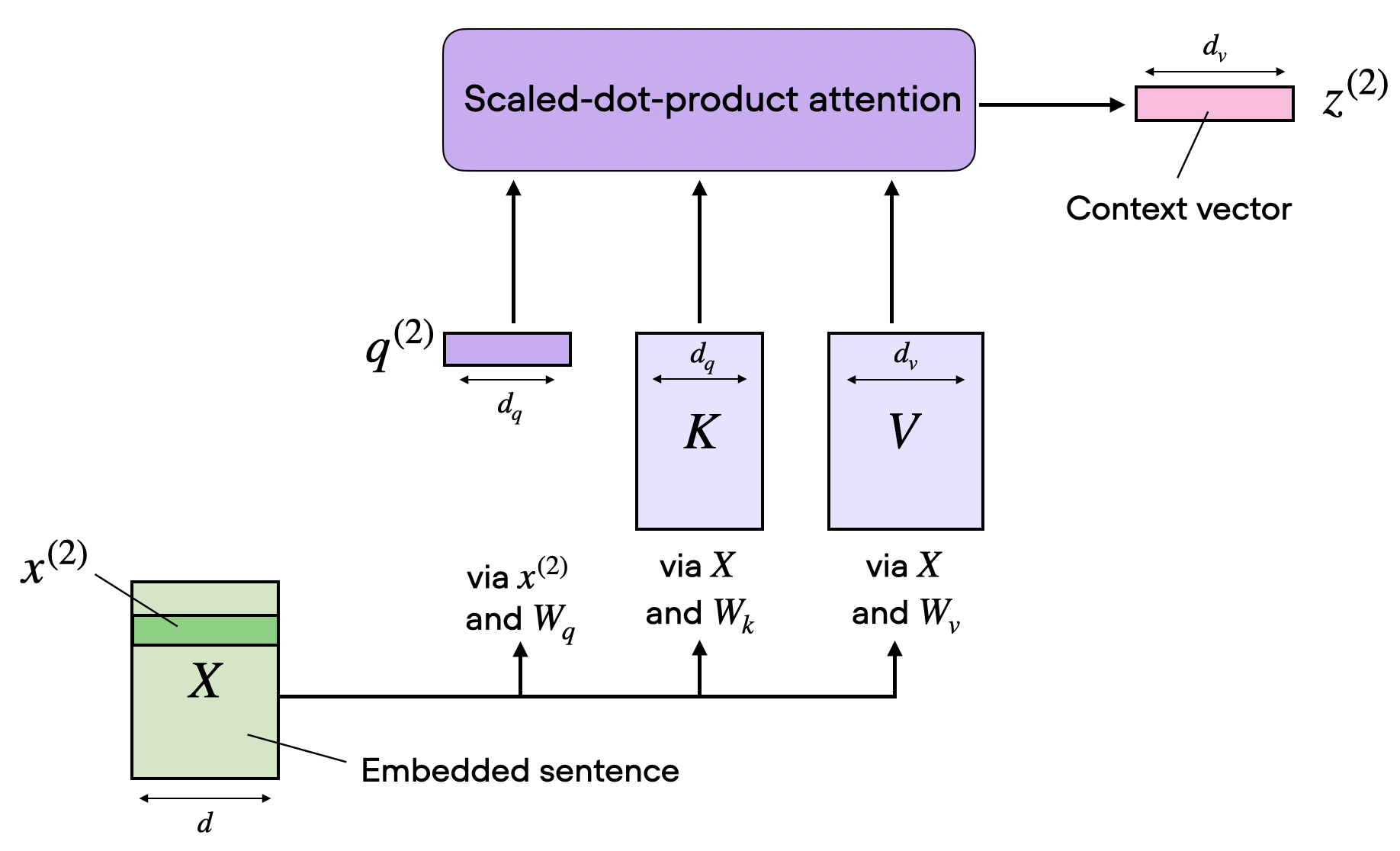
A single self-attention head
Now create a \(n_{words} \cdot dim_{word_{embedding}} = 8 \cdot 16\) embedding tensor.
These initial values will be randomly generated and \(\dim_{vec} = 16\) is an hyper-parameter.
embedding_layer = torch.nn.Embedding(n_sentence, dim_word_embedding)
embedded_sentence = embedding_layer(sentence_ints).detach()
print('Embedded sentence shape =', embedded_sentence.shape)
Embedded sentence shape = torch.Size([8, 16])
Let’s choose values for Queries, Keys, and Values. Since Queries and Keys vector are multiplied afterward, their dimensions MUST be equal.
dim_q, dim_v = 24, 28
dim_k = dim_q
W_q = torch.rand(dim_q, dim_word_embedding)
W_k = torch.rand(dim_k, dim_word_embedding)
W_v = torch.rand(dim_v, dim_word_embedding)
Compute queries, keys, values for the input words
First, try to understand this on single words.
Example #1
Compute query, key, and value vector related to the first and second words in the sentence (\(idx = 0, 1\)).
word_idx = 0
x_1 = embedded_sentence[word_idx]
query_1 = W_q @ x_1
key_1 = W_k @ x_1
value_1 = W_v @ x_1
print('Word idx =', word_idx)
print('\tQuery size =', query_1.shape)
print('\tKey size =', key_1.shape)
print('\tValue size =', value_1.shape)
Word idx = 0
Query size = torch.Size([24])
Key size = torch.Size([24])
Value size = torch.Size([28])
word_idx = 1
x_2 = embedded_sentence[word_idx]
query_2 = W_q @ x_2
key_2 = W_k @ x_2
value_2 = W_v @ x_2
print('Word idx =', word_idx)
print('\tQuery size =', query_2.shape)
print('\tKey size =', key_2.shape)
print('\tValue size =', value_2.shape)
Word idx = 1
Query size = torch.Size([24])
Key size = torch.Size([24])
Value size = torch.Size([28])
Compute queries, keys, values for ALL input words
Now that I have understood the process, let’s extend this to all the input words. Transpose the matrices to have words on rows and vector components on columns.
queries = (W_q @ embedded_sentence.T).T
keys = (W_k @ embedded_sentence.T).T
values = (W_v @ embedded_sentence.T).T
print('All input words -> queries.shape =', queries.shape)
print('All input words -> keys.shape =', keys.shape)
print('All input words -> values.shape =', values.shape)
All input words -> queries.shape = torch.Size([8, 24])
All input words -> keys.shape = torch.Size([8, 24])
All input words -> values.shape = torch.Size([8, 28])
Unnormalized attention scores
As before, I am trying to understand this concept on single words.
Example #2
Let’s compute the unnormalized attention score \(\omega\) (omega) for the first word w.r.t. the 5th word
omega_1_5 = queries[0] @ keys[4]
print('Unnormalized attention score of first word w.r.t. 5th word =', omega_1_5.item())
Unnormalized attention score of first word w.r.t. 5th word = -46.02456283569336
Compute unnormalized attention scores w.r.t. ALL input words
Let’s compute the unnormalized attention scores for the first word w.r.t. to all other words.
omega_1_all = queries[0] @ keys.T
print(f'Unnormalized attention scores of first word w.r.t. ALL other words:\n{omega_1_all}')
Unnormalized attention scores of first word w.r.t. ALL other words:
tensor([ 47.9667, 58.9805, 42.1271, 141.0643, -46.0246, -72.1767, 58.9805,
47.9667])
Compute unnormalized attention scores for ALL input words
Let’s compute the unnormalized attention scores for all the words w.r.t. to all other words.
omega_all = queries @ keys.T
print(f'Unnormalized attention scores of ALL words w.r.t. ALL other words:\n{omega_all}')
print("All input words scores -> omega_all.shape =", omega_all.shape)
Unnormalized attention scores of ALL words w.r.t. ALL other words:
tensor([[ 47.9667, 58.9805, 42.1272, 141.0642, -46.0246, -72.1767,
58.9805, 47.9667],
[ 58.7503, 93.6661, 65.4516, 229.0244, -51.6797, -109.5712,
93.6661, 58.7503],
[ 47.7602, 53.6036, 42.4971, 132.3753, -45.4809, -63.6152,
53.6036, 47.7602],
[ 145.1907, 182.7591, 157.4097, 479.7147, -139.6413, -238.2749,
182.7591, 145.1907],
[ -26.0050, -25.1779, -21.8697, -61.3257, 20.7895, 35.2284,
-25.1779, -26.0050],
[ -71.2604, -94.5636, -83.3776, -257.1654, 66.7258, 130.5431,
-94.5636, -71.2604],
[ 58.7503, 93.6661, 65.4516, 229.0244, -51.6797, -109.5712,
93.6661, 58.7503],
[ 47.9667, 58.9805, 42.1272, 141.0642, -46.0246, -72.1767,
58.9805, 47.9667]])
All input words scores -> omega_all.shape = torch.Size([8, 8])
Normalized attention scores
Why? To reach more numeric stability and thus, reduce errors. Note that the sum of the values is 1 (thanks to the softmax function).
Example #3
Let’s compute the normalized attention score \(\alpha\) (alpha) for the first word w.r.t. the ALL other words.
normalized_attention_scores_1 = F.softmax(omega_1_all / dim_k ** 0.5, dim=0)
print(f'Normalized attention scores of first word w.r.t. ALL other words:\n{normalized_attention_scores_1}')
print('Sum of this vector =', normalized_attention_scores_1.sum().item())
Normalized attention scores of first word w.r.t. ALL other words:
tensor([5.5834e-09, 5.2879e-08, 1.6952e-09, 1.0000e+00, 2.5976e-17, 1.2479e-19,
5.2879e-08, 5.5834e-09])
Sum of this vector = 1.0
Compute normalized attention scores for ALL input words
Let’s compute the normalized attention score \(\alpha\) (alpha) for ALL words w.r.t. ALL other words.
normalized_attention_scores = F.softmax(omega_all / dim_k ** 0.5, dim=0)
print(f'Normalized attention scores of ALL words w.r.t. ALL other words:\n{normalized_attention_scores}')
print('Sum of this vector =', normalized_attention_scores.sum().item())
Normalized attention scores of ALL words w.r.t. ALL other words:
tensor([[2.4049e-09, 1.0642e-11, 6.0284e-11, 9.5202e-31, 1.0108e-10, 1.0688e-18,
1.0642e-11, 2.4049e-09],
[2.1730e-08, 1.2645e-08, 7.0456e-09, 5.9746e-23, 3.1866e-11, 5.1745e-22,
1.2645e-08, 2.1730e-08],
[2.3056e-09, 3.5511e-12, 6.5013e-11, 1.6157e-31, 1.1294e-10, 6.1358e-18,
3.5511e-12, 2.3056e-09],
[1.0000e+00, 1.0000e+00, 1.0000e+00, 1.0000e+00, 5.0760e-19, 2.0151e-33,
1.0000e+00, 1.0000e+00],
[6.6606e-16, 3.6846e-19, 1.2790e-16, 0.0000e+00, 8.4667e-05, 3.5510e-09,
3.6846e-19, 6.6606e-16],
[6.4806e-20, 2.6022e-25, 4.5103e-22, 0.0000e+00, 9.9992e-01, 1.0000e+00,
2.6022e-25, 6.4806e-20],
[2.1730e-08, 1.2645e-08, 7.0456e-09, 5.9747e-23, 3.1866e-11, 5.1745e-22,
1.2645e-08, 2.1730e-08],
[2.4049e-09, 1.0642e-11, 6.0284e-11, 9.5202e-31, 1.0108e-10, 1.0688e-18,
1.0642e-11, 2.4049e-09]])
Sum of this vector = 8.0
## Compute \(z\) vector The \(z\) vector is an enhanced version of the input word. In other words, it “embeds” the information about ALL the other inputs words.
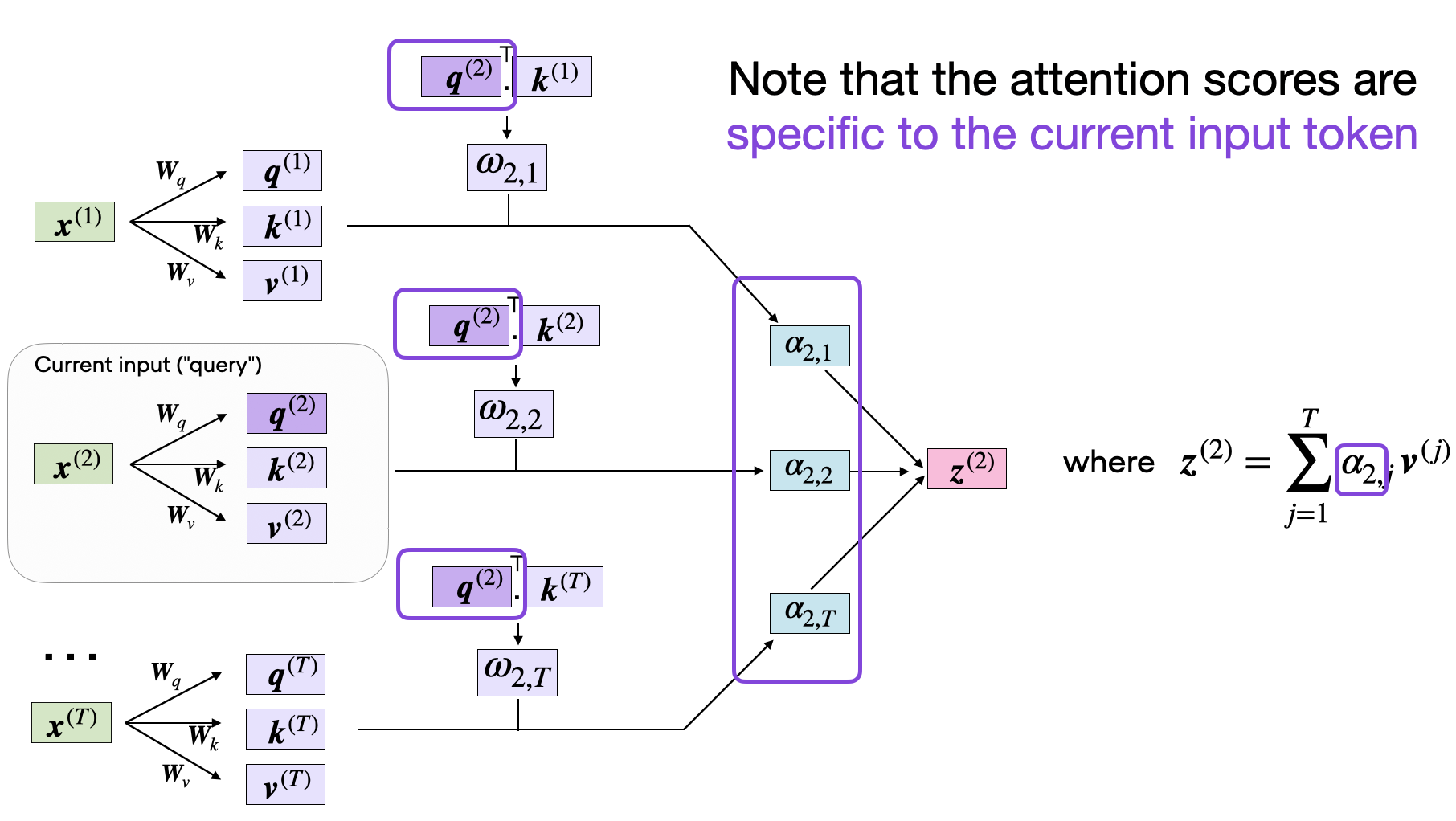
The context vector
Note that the dimension of \(z = dim_v\), and in this case \(dim_v > dim_{word_{embedding}}\), but it turns out that can be arbitrarly chosen.
Example #4
Let’s compute \(z\) for the first word w.r.t. ALL other words.
context_vector_z_1 = normalized_attention_scores_1 @ values
print('Context vector related to the first word w.r.t. ALL other words')
print('Shape =', context_vector_z_1.shape)
print(context_vector_z_1)
Context vector related to the first word w.r.t. ALL other words
Shape = torch.Size([28])
tensor([5.2083, 4.5906, 3.1900, 4.1853, 4.7579, 4.2178, 3.4120, 5.0137, 4.0621,
4.1455, 6.3549, 3.0836, 6.4934, 4.0425, 4.8676, 3.0821, 6.8482, 5.5784,
4.6929, 5.4580, 5.6707, 4.9629, 4.2686, 5.6802, 5.3528, 4.5219, 4.6112,
4.7807])
Compute \(z\) for ALL input words
Let’s compute \(z\) for ALL words w.r.t. ALL other words.
context_z = normalized_attention_scores @ values
print('Context vector related to ALL input words w.r.t. ALL other words')
print('Shape =', context_z.shape)
print(context_z)
Context vector related to ALL input words w.r.t. ALL other words
Shape = torch.Size([8, 28])
tensor([[ 1.0208e-08, 4.5245e-09, 8.9584e-09, 8.8031e-09, 1.0888e-08,
1.1263e-08, 6.6825e-09, 9.1426e-09, 3.3903e-09, 9.7982e-09,
1.1035e-08, 4.7999e-09, 1.4235e-08, 1.4572e-08, 6.5525e-09,
7.8531e-09, 8.0995e-09, 1.5258e-08, 1.1228e-09, 1.2500e-08,
1.6545e-09, 8.0533e-09, 1.2058e-08, 1.8843e-09, 1.4327e-08,
1.2405e-08, 1.1857e-09, 1.0192e-08],
[ 1.3333e-07, 1.4292e-07, 1.4621e-07, 5.8652e-08, 9.4583e-08,
2.0076e-07, 1.0602e-07, 1.5732e-07, 9.1718e-08, 1.1024e-07,
1.1862e-07, 5.8737e-08, 1.7114e-07, 1.5896e-07, 1.0163e-07,
9.6130e-08, 1.6256e-07, 2.0144e-07, 6.1971e-08, 1.4980e-07,
5.8659e-08, 1.8701e-07, 1.8030e-07, 9.1482e-08, 1.2541e-07,
1.3888e-07, 7.5303e-08, 1.3610e-07],
[ 9.7775e-09, 4.3164e-09, 8.5718e-09, 8.4555e-09, 1.0414e-08,
1.0743e-08, 6.3774e-09, 8.7203e-09, 3.2221e-09, 9.3672e-09,
1.0560e-08, 4.5993e-09, 1.3607e-08, 1.3972e-08, 6.2539e-09,
7.5503e-09, 7.7105e-09, 1.4573e-08, 1.0270e-09, 1.1957e-08,
1.5478e-09, 7.6659e-09, 1.1533e-08, 1.7809e-09, 1.3734e-08,
1.1868e-08, 1.1197e-09, 9.7389e-09],
[ 1.3486e+01, 1.5032e+01, 1.2241e+01, 6.8524e+00, 1.0054e+01,
1.7727e+01, 1.0002e+01, 1.5045e+01, 1.0787e+01, 1.0733e+01,
1.3517e+01, 7.1050e+00, 1.6438e+01, 1.3163e+01, 1.2065e+01,
8.8727e+00, 1.8247e+01, 1.7620e+01, 9.5952e+00, 1.4581e+01,
1.0128e+01, 1.7828e+01, 1.5626e+01, 1.3258e+01, 1.2085e+01,
1.2815e+01, 1.0607e+01, 1.3737e+01],
[-2.8815e-05, 1.2425e-04, 8.1114e-05, -6.0943e-05, -2.9221e-04,
-1.4321e-04, -5.3928e-05, -7.0047e-05, -3.8643e-05, -1.8990e-04,
-1.9285e-04, -7.4484e-05, -1.9050e-04, -2.8142e-05, -1.7792e-04,
1.2690e-04, -1.6557e-04, -2.0935e-04, -1.6793e-04, -1.7158e-04,
-1.2642e-04, -2.8246e-05, -3.0229e-05, -3.8677e-05, -1.6634e-04,
-1.9244e-04, 4.7392e-05, -2.1519e-04],
[-2.0627e+00, -1.8042e+00, -5.9498e-02, -3.8449e+00, -6.9198e+00,
-2.7874e+00, -2.7707e+00, -2.4009e+00, -4.4370e+00, -5.5688e+00,
-4.6235e+00, -2.1498e+00, -1.5360e+00, -7.4642e-01, -5.4877e+00,
-6.5154e-01, -3.2329e+00, -3.8940e+00, -5.0657e+00, -2.5105e+00,
-7.0453e+00, -2.9677e+00, -1.5344e+00, -2.5249e+00, -5.9545e+00,
-2.9639e+00, -2.7855e+00, -5.6987e+00],
[ 1.3333e-07, 1.4291e-07, 1.4621e-07, 5.8652e-08, 9.4584e-08,
2.0076e-07, 1.0602e-07, 1.5732e-07, 9.1717e-08, 1.1024e-07,
1.1862e-07, 5.8737e-08, 1.7114e-07, 1.5896e-07, 1.0163e-07,
9.6130e-08, 1.6256e-07, 2.0144e-07, 6.1971e-08, 1.4980e-07,
5.8659e-08, 1.8701e-07, 1.8030e-07, 9.1482e-08, 1.2541e-07,
1.3888e-07, 7.5303e-08, 1.3610e-07],
[ 1.0208e-08, 4.5245e-09, 8.9584e-09, 8.8031e-09, 1.0888e-08,
1.1263e-08, 6.6825e-09, 9.1426e-09, 3.3903e-09, 9.7982e-09,
1.1035e-08, 4.7999e-09, 1.4235e-08, 1.4572e-08, 6.5525e-09,
7.8531e-09, 8.0995e-09, 1.5258e-08, 1.1228e-09, 1.2500e-08,
1.6545e-09, 8.0533e-09, 1.2058e-08, 1.8843e-09, 1.4327e-08,
1.2405e-08, 1.1857e-09, 1.0192e-08]])
Ok but…are you getting confused by all these dimension?
Try to check out this picture.
A single self-attention head
Multi-head self-attention
Each query has now shape \(n_{heads} \times dim_{word_{embedding}}\).
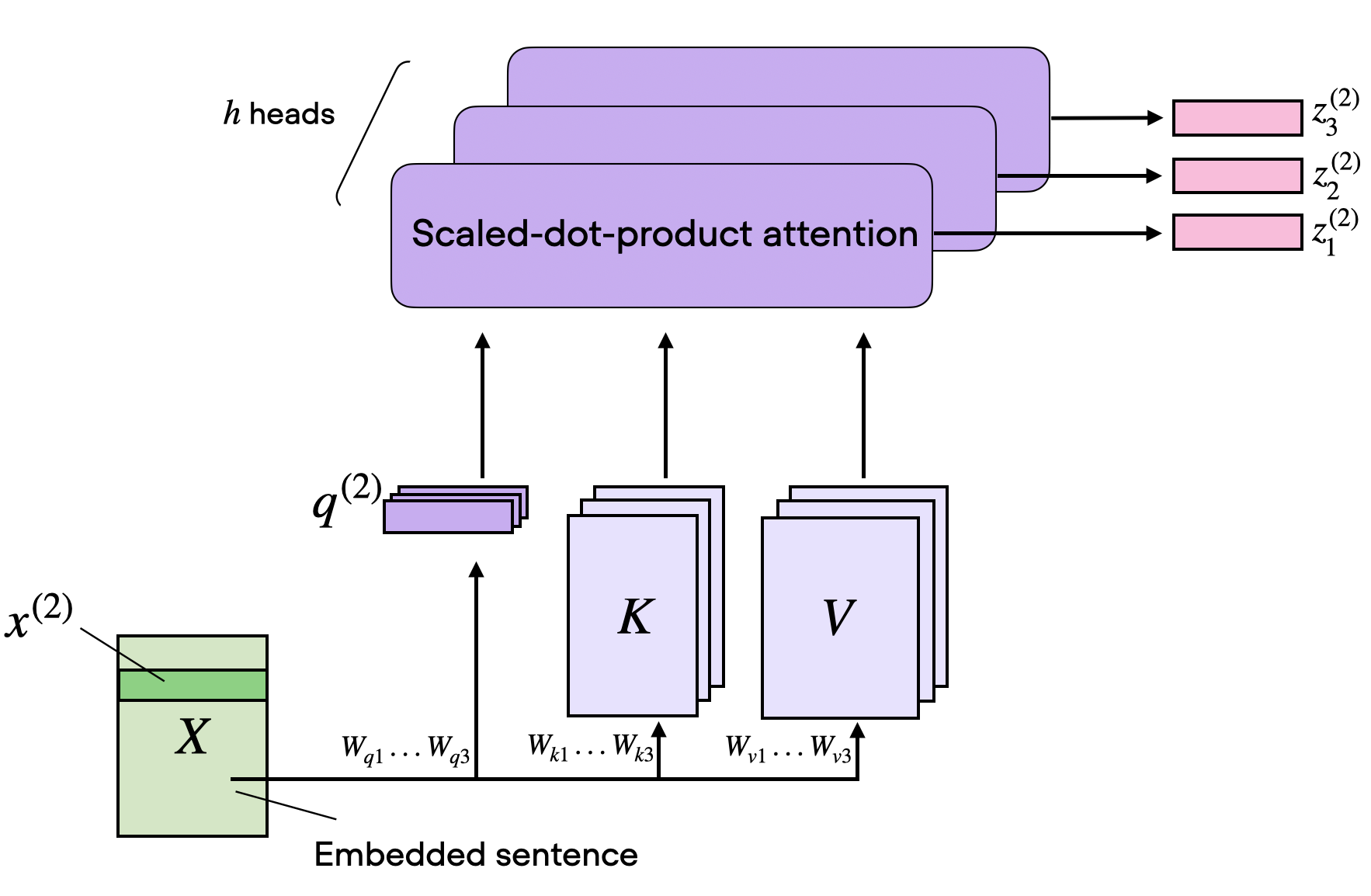
A multi self-attention head
n_heads = 3
multihead_W_query = torch.rand(n_heads, dim_q, dim_word_embedding)
multihead_W_key = torch.rand(n_heads, dim_k, dim_word_embedding)
multihead_W_value = torch.rand(n_heads, dim_v, dim_word_embedding)
Follow this example with the first word.
word_idx = 0
x_1 = embedded_sentence[word_idx]
multihead_query_1 = multihead_W_query @ x_1
multihead_key_1 = multihead_W_key @ x_1
multihead_value_1 = multihead_W_value @ x_1
print('Word idx =', word_idx)
print('\tMultihead-query size =', multihead_query_1.shape)
print('\tMultihead-key size =', multihead_key_1.shape)
print('\tMultihead-value size =', multihead_value_1.shape)
Word idx = 0
Multihead-query size = torch.Size([3, 24])
Multihead-key size = torch.Size([3, 24])
Multihead-value size = torch.Size([3, 28])
But for extend this example to all the words, we have to use the bmm() (Batch Matrix Mutliplication) method from PyTorch. It’s useful when there’s the need to deal with tensor. The effective matmulis performed along the last two dimensions, while the first one representing heads is preserved.
Finally, to make the input feasible (i.e., choose the right dimensions) for the multi-head attention layer, I need to replicate it for the number of attention heads (in this case, three times).
repeated_inputs = embedded_sentence.T.repeat(n_heads, 1, 1)
print('Repeated input size =', repeated_inputs.shape)
Repeated input size = torch.Size([3, 16, 8])
multihead_queries = torch.bmm(multihead_W_query, repeated_inputs)
multihead_keys = torch.bmm(multihead_W_key, repeated_inputs)
multihead_values = torch.bmm(multihead_W_value, repeated_inputs)
print('All input words -> multihead_queries.shape =', multihead_queries.shape)
print('All input words -> multihead_keys.shape =', multihead_keys.shape)
print('All input words -> multihead_values.shape =', multihead_values.shape)
All input words -> multihead_queries.shape = torch.Size([3, 24, 8])
All input words -> multihead_keys.shape = torch.Size([3, 24, 8])
All input words -> multihead_values.shape = torch.Size([3, 28, 8])
But - as can be seen from above - the last two dimensions are swapped, because I would like to have words as the second dimension and vector components as third one. Hence, let’s permute (i.e., swap) the last two dimensions.
Here, the permute() method is asking the desidered ordering of dimensions.
multihead_queries = multihead_queries.permute(0, 2, 1)
multihead_keys = multihead_keys.permute(0, 2, 1)
multihead_values = multihead_values.permute(0, 2, 1)
print('All input words -> multihead_queries.shape =', multihead_queries.shape)
print('All input words -> multihead_keys.shape =', multihead_keys.shape)
print('All input words -> multihead_values.shape =', multihead_values.shape)
All input words -> multihead_queries.shape = torch.Size([3, 8, 24])
All input words -> multihead_keys.shape = torch.Size([3, 8, 24])
All input words -> multihead_values.shape = torch.Size([3, 8, 28])
Compute unnormalized attention scores
As did before, compute the unnormalzied attention scores for each head.
multihead_omega_all = torch.bmm(multihead_queries, multihead_keys.permute(0,2,1))
print(f'Unnormalized attention scores of ALL words w.r.t. ALL other words:\n{multihead_omega_all}')
print("All input words scores -> omega_all.shape =", multihead_omega_all.shape)
Unnormalized attention scores of ALL words w.r.t. ALL other words:
tensor([[[ 63.3466, 69.7982, 60.7684, 168.7238, -35.8708, -90.1632,
69.7982, 63.3466],
[ 64.3794, 50.0433, 56.6445, 156.4643, -33.4781, -78.7985,
50.0433, 64.3794],
[ 54.1203, 63.1504, 53.7396, 154.9160, -35.4911, -82.0983,
63.1504, 54.1203],
[ 178.0788, 180.1088, 162.0738, 483.6229, -87.1213, -246.8582,
180.1088, 178.0788],
[ -27.7026, -43.6290, -35.4398, -103.1395, 30.3216, 52.3912,
-43.6290, -27.7026],
[ -76.8325, -87.6214, -66.1114, -224.5666, 31.7686, 111.7955,
-87.6214, -76.8325],
[ 64.3794, 50.0433, 56.6445, 156.4643, -33.4781, -78.7985,
50.0433, 64.3794],
[ 63.3466, 69.7982, 60.7684, 168.7238, -35.8708, -90.1632,
69.7982, 63.3466]],
[[ 40.2509, 51.2320, 37.3632, 140.1730, -24.4904, -60.2304,
51.2320, 40.2509],
[ 54.8854, 63.9741, 42.0731, 159.9941, -37.8272, -62.2964,
63.9741, 54.8854],
[ 45.0314, 58.8531, 46.1473, 171.9726, -39.9998, -75.0010,
58.8531, 45.0314],
[ 147.8137, 211.9995, 141.7101, 559.7228, -125.7353, -237.5117,
211.9995, 147.8137],
[ -36.2802, -40.3992, -36.5809, -128.0536, 31.7833, 45.6996,
-40.3992, -36.2802],
[ -70.0388, -124.8755, -72.3371, -282.8608, 65.5955, 124.3698,
-124.8755, -70.0388],
[ 54.8854, 63.9741, 42.0731, 159.9941, -37.8272, -62.2964,
63.9741, 54.8854],
[ 40.2509, 51.2320, 37.3632, 140.1730, -24.4904, -60.2304,
51.2320, 40.2509]],
[[ 62.2692, 34.5424, 52.8352, 160.1184, -40.1587, -68.9696,
34.5424, 62.2692],
[ 72.3984, 51.9031, 57.8771, 202.6503, -44.1590, -101.3688,
51.9031, 72.3984],
[ 52.9430, 40.0645, 43.6347, 147.3360, -31.0522, -61.0057,
40.0645, 52.9430],
[ 139.6398, 107.2641, 127.2303, 425.1722, -99.6243, -196.1776,
107.2641, 139.6398],
[ -27.6845, -25.2708, -27.7060, -81.5897, 25.3154, 31.5857,
-25.2708, -27.6845],
[ -83.8774, -66.2358, -70.5194, -238.9998, 54.5963, 106.6016,
-66.2358, -83.8774],
[ 72.3984, 51.9031, 57.8771, 202.6503, -44.1590, -101.3688,
51.9031, 72.3984],
[ 62.2692, 34.5424, 52.8352, 160.1184, -40.1587, -68.9696,
34.5424, 62.2692]]])
All input words scores -> omega_all.shape = torch.Size([3, 8, 8])
Compute normalized attention scores for ALL input words
Let’s compute the normalized attention score \(\alpha\) (alpha) for ALL words w.r.t. ALL other words.
multihead_normalized_attention_scores = F.softmax(multihead_omega_all / dim_k ** 0.5, dim=0)
print(f'Multihead normalized attention scores of ALL words w.r.t. ALL other words:\n{multihead_normalized_attention_scores}')
print('Sum of this vector =', multihead_normalized_attention_scores.sum().item())
Multihead normalized attention scores of ALL words w.r.t. ALL other words:
tensor([[[5.5202e-01, 9.7718e-01, 8.2888e-01, 8.5065e-01, 8.6035e-02,
1.8976e-03, 9.7718e-01, 5.5202e-01],
[1.5916e-01, 5.0917e-02, 4.2787e-01, 8.0445e-05, 6.5592e-01,
3.3284e-02, 5.0917e-02, 1.5916e-01],
[5.1472e-01, 7.0178e-01, 7.4659e-01, 2.9650e-02, 2.5820e-01,
1.2600e-02, 7.0178e-01, 5.1472e-01],
[9.9754e-01, 1.4868e-03, 9.8379e-01, 1.7937e-07, 9.2739e-01,
3.2141e-05, 1.4868e-03, 9.9754e-01],
[4.5928e-01, 2.2055e-02, 1.5059e-01, 1.2142e-02, 3.6933e-01,
7.8774e-01, 2.2055e-02, 4.5928e-01],
[1.9087e-01, 1.2551e-02, 5.9268e-01, 9.5008e-01, 9.0600e-04,
6.9592e-02, 1.2551e-02, 1.9087e-01],
[1.5916e-01, 5.0917e-02, 4.2787e-01, 8.0445e-05, 6.5592e-01,
3.3284e-02, 5.0917e-02, 1.5916e-01],
[5.5202e-01, 9.7718e-01, 8.2888e-01, 8.5065e-01, 8.6035e-02,
1.8976e-03, 9.7718e-01, 5.5202e-01]],
[[4.9490e-03, 2.2084e-02, 6.9762e-03, 2.5045e-03, 8.7811e-01,
8.5455e-01, 2.2084e-02, 4.9490e-03],
[2.2918e-02, 8.7465e-01, 2.1855e-02, 1.6536e-04, 2.6996e-01,
9.6638e-01, 8.7465e-01, 2.2918e-02],
[8.0509e-02, 2.9191e-01, 1.5850e-01, 9.6404e-01, 1.0286e-01,
5.3648e-02, 2.9191e-01, 8.0509e-02],
[2.0698e-03, 9.9851e-01, 1.5405e-02, 1.0000e+00, 3.5005e-04,
2.1658e-04, 9.9851e-01, 2.0698e-03],
[7.9740e-02, 4.2640e-02, 1.1930e-01, 7.5100e-05, 4.9774e-01,
2.0099e-01, 4.2640e-02, 7.9740e-02],
[7.6382e-01, 6.2532e-06, 1.6631e-01, 6.4562e-06, 9.0342e-01,
9.0630e-01, 6.2532e-06, 7.6382e-01],
[2.2918e-02, 8.7465e-01, 2.1855e-02, 1.6536e-04, 2.6996e-01,
9.6638e-01, 8.7465e-01, 2.2918e-02],
[4.9490e-03, 2.2084e-02, 6.9762e-03, 2.5045e-03, 8.7811e-01,
8.5455e-01, 2.2084e-02, 4.9490e-03]],
[[4.4303e-01, 7.3207e-04, 1.6414e-01, 1.4685e-01, 3.5855e-02,
1.4355e-01, 7.3207e-04, 4.4303e-01],
[8.1792e-01, 7.4429e-02, 5.5028e-01, 9.9975e-01, 7.4127e-02,
3.3219e-04, 7.4429e-02, 8.1792e-01],
[4.0477e-01, 6.3044e-03, 9.4906e-02, 6.3105e-03, 6.3894e-01,
9.3375e-01, 6.3044e-03, 4.0477e-01],
[3.9022e-04, 5.1828e-10, 8.0173e-04, 1.1806e-12, 7.2256e-02,
9.9975e-01, 5.1828e-10, 3.9022e-04],
[4.6098e-01, 9.3530e-01, 7.3012e-01, 9.8778e-01, 1.3293e-01,
1.1271e-02, 9.3530e-01, 4.6098e-01],
[4.5311e-02, 9.8744e-01, 2.4102e-01, 4.9918e-02, 9.5677e-02,
2.4106e-02, 9.8744e-01, 4.5311e-02],
[8.1792e-01, 7.4429e-02, 5.5028e-01, 9.9975e-01, 7.4127e-02,
3.3219e-04, 7.4429e-02, 8.1792e-01],
[4.4303e-01, 7.3207e-04, 1.6414e-01, 1.4685e-01, 3.5855e-02,
1.4355e-01, 7.3207e-04, 4.4303e-01]]])
Sum of this vector = 64.0
Compute \(z\) for ALL input words
Let’s compute \(z\) for ALL words w.r.t. ALL other words.
multihead_context_z = multihead_normalized_attention_scores @ multihead_values
print('Multihead context vector related to ALL input words w.r.t. ALL other words')
print('Shape =', multihead_context_z.shape)
print(multihead_context_z)
Multihead context vector related to ALL input words w.r.t. ALL other words
Shape = torch.Size([3, 8, 28])
tensor([[[ 1.2550e+01, 8.2323e+00, 9.1246e+00, 2.9574e+00, 1.3149e+01,
1.1474e+01, 5.4783e+00, 8.9908e+00, 8.1721e+00, 9.5334e+00,
1.2736e+01, 1.0823e+01, 1.4178e+01, 1.3128e+01, 1.0271e+01,
7.1355e+00, 9.9221e+00, 1.1401e+01, 9.2407e+00, 8.2230e+00,
1.4161e+01, 1.2087e+01, 5.3284e+00, 1.3517e+01, 1.0876e+01,
1.0542e+01, 1.3312e+01, 9.9359e+00],
[ 8.4613e-01, 5.4901e-01, -9.3701e-01, -5.6394e-02, 1.7809e-01,
6.3644e-01, 3.3348e-01, -6.3719e-02, 7.8778e-01, 4.3655e-01,
5.3653e-01, 6.2437e-01, 7.7565e-01, -5.2384e-01, -1.3249e-01,
5.0235e-01, 1.7263e-01, 9.4807e-01, -1.7731e-01, 8.8894e-02,
9.8492e-02, 6.2525e-01, -1.3491e+00, 1.0078e+00, 5.1598e-01,
-1.0351e+00, 7.7803e-01, 1.1364e+00],
[ 6.7393e+00, 4.8771e+00, 3.2697e+00, 4.0000e-01, 6.6771e+00,
6.5647e+00, 1.8090e+00, 4.0669e+00, 2.9440e+00, 4.5260e+00,
6.0300e+00, 5.4758e+00, 8.6360e+00, 6.0929e+00, 4.9760e+00,
3.3591e+00, 4.7602e+00, 6.6984e+00, 3.2040e+00, 4.1491e+00,
7.3087e+00, 6.6017e+00, -3.4923e-01, 7.0143e+00, 4.2075e+00,
4.8420e+00, 6.6773e+00, 5.5571e+00],
[ 2.7140e+00, 4.7744e+00, 1.2109e+00, 4.0982e+00, 5.1366e+00,
4.2388e+00, 2.9954e+00, 4.2085e+00, 1.1205e+00, 5.9954e-01,
3.1774e-01, 7.3186e+00, 6.3972e+00, 1.9380e+00, 5.1665e+00,
1.1845e+00, 4.1889e+00, 5.8980e+00, 3.1623e+00, 4.1146e+00,
4.7828e+00, 3.5414e+00, -2.6044e+00, 3.4029e+00, 3.0947e+00,
2.5684e+00, 1.9649e+00, 3.0005e+00],
[-1.9108e+00, -7.5741e-01, -1.6170e+00, -4.9262e-01, -1.3816e-01,
-1.6101e+00, -2.3048e-01, 1.2725e+00, -2.9797e+00, -3.0562e+00,
-1.5322e+00, 1.6294e+00, 1.2837e+00, 1.6719e-01, -1.0773e+00,
-1.5306e+00, -8.8325e-01, 1.2672e+00, -1.8476e+00, 1.0466e+00,
-7.4326e-01, -1.3275e+00, -4.3374e+00, 7.7009e-01, -4.2708e-01,
-8.8085e-01, -1.6558e+00, 1.1952e+00],
[ 4.7833e+00, 4.2254e+00, 6.5103e+00, 4.6408e+00, 7.3923e+00,
4.5949e+00, 5.0826e+00, 6.4071e+00, 4.6354e+00, 4.2027e+00,
5.3380e+00, 7.5981e+00, 6.1271e+00, 6.7390e+00, 6.8821e+00,
3.3658e+00, 6.1592e+00, 5.8023e+00, 7.0229e+00, 5.0363e+00,
7.9460e+00, 5.2522e+00, 5.7094e+00, 6.2701e+00, 7.7611e+00,
6.6257e+00, 5.8532e+00, 4.3290e+00],
[ 8.4613e-01, 5.4901e-01, -9.3701e-01, -5.6395e-02, 1.7809e-01,
6.3644e-01, 3.3348e-01, -6.3719e-02, 7.8778e-01, 4.3655e-01,
5.3653e-01, 6.2437e-01, 7.7565e-01, -5.2384e-01, -1.3249e-01,
5.0235e-01, 1.7263e-01, 9.4807e-01, -1.7731e-01, 8.8894e-02,
9.8493e-02, 6.2525e-01, -1.3491e+00, 1.0078e+00, 5.1598e-01,
-1.0351e+00, 7.7803e-01, 1.1364e+00],
[ 1.2550e+01, 8.2323e+00, 9.1246e+00, 2.9574e+00, 1.3149e+01,
1.1474e+01, 5.4783e+00, 8.9908e+00, 8.1721e+00, 9.5334e+00,
1.2736e+01, 1.0823e+01, 1.4178e+01, 1.3128e+01, 1.0271e+01,
7.1355e+00, 9.9221e+00, 1.1401e+01, 9.2407e+00, 8.2230e+00,
1.4161e+01, 1.2087e+01, 5.3284e+00, 1.3517e+01, 1.0876e+01,
1.0542e+01, 1.3312e+01, 9.9359e+00]],
[[-3.0829e+00, -4.3344e+00, -3.8598e+00, -2.1292e+00, -2.6663e+00,
-1.8364e+00, 2.5687e-01, -6.3279e+00, -3.2069e+00, -3.2803e+00,
-1.0921e+00, -4.5912e+00, -6.8437e-01, 3.7830e-01, -3.6839e-01,
-2.0829e+00, -2.6025e+00, -4.2082e+00, -4.3396e+00, -2.9734e+00,
-2.1751e+00, -3.2557e+00, -9.7399e-01, -1.9781e+00, -1.0855e+00,
-1.8056e+00, -2.5949e+00, -4.7041e+00],
[ 3.0845e+00, -9.0204e-01, -3.8693e+00, 4.5435e-03, 1.5541e-01,
-2.5049e+00, 4.0231e+00, -6.7520e+00, -1.5541e+00, -5.8121e-01,
2.5355e+00, -2.8262e+00, 1.5110e+00, 2.3968e+00, 5.0290e+00,
-7.1024e-02, -1.2569e+00, -1.7446e+00, -1.8978e+00, -1.9663e-02,
1.5819e+00, -2.5593e+00, 4.8311e-01, -1.4362e+00, 8.9585e-01,
2.2621e-01, -6.3192e-01, 9.6575e-01],
[ 5.2792e+00, 5.8114e+00, 3.1216e+00, 4.8434e+00, 6.1506e+00,
4.7512e+00, 6.1214e+00, 5.1191e+00, 3.7631e+00, 5.7305e+00,
6.5150e+00, 4.5658e+00, 4.9792e+00, 4.2492e+00, 7.3722e+00,
6.2548e+00, 3.7377e+00, 4.4937e+00, 5.0615e+00, 5.5706e+00,
6.0054e+00, 5.2596e+00, 4.5952e+00, 3.2967e+00, 4.7211e+00,
4.6390e+00, 4.1446e+00, 6.8238e+00],
[ 9.5750e+00, 7.7102e+00, 2.6211e+00, 6.1118e+00, 9.5336e+00,
3.7211e+00, 9.6168e+00, 3.6955e+00, 3.9494e+00, 7.2018e+00,
9.3044e+00, 5.1696e+00, 6.6733e+00, 5.4449e+00, 1.1458e+01,
5.9527e+00, 4.9379e+00, 5.7139e+00, 6.2403e+00, 6.1889e+00,
9.8552e+00, 4.8115e+00, 4.9289e+00, 3.1193e+00, 5.1594e+00,
4.8541e+00, 6.3040e+00, 9.4579e+00],
[-5.6094e-01, -1.1267e+00, -8.5515e-01, -5.0801e-01, -3.0618e-01,
2.7183e-02, 6.2272e-01, -1.9285e+00, -7.3523e-01, -8.9529e-01,
2.9595e-02, -1.2084e+00, 4.0297e-01, 9.4168e-01, 4.5556e-01,
-5.4734e-01, -1.0261e-01, -1.3311e+00, -1.2880e+00, -7.8507e-01,
-7.4631e-01, -7.8153e-01, -7.5138e-02, -2.1338e-01, -1.2993e-01,
-8.4351e-01, -3.6570e-01, -1.5080e+00],
[-7.4788e-01, -1.7038e+00, -1.7669e+00, -2.7876e-01, -2.6155e+00,
2.2724e+00, 1.1839e+00, -3.0407e+00, 8.9993e-01, -1.0570e+00,
-1.9050e-01, -2.6671e+00, 1.6860e+00, 4.7182e+00, 3.1012e+00,
3.2457e+00, -2.4241e-01, -3.0754e+00, -2.5329e+00, 1.5982e+00,
-5.2954e+00, -6.2323e-01, 1.4935e+00, 1.3279e+00, 3.0294e+00,
9.1379e-01, -2.9769e+00, -5.4288e-01],
[ 3.0845e+00, -9.0205e-01, -3.8693e+00, 4.5432e-03, 1.5541e-01,
-2.5049e+00, 4.0231e+00, -6.7520e+00, -1.5541e+00, -5.8121e-01,
2.5355e+00, -2.8262e+00, 1.5110e+00, 2.3968e+00, 5.0290e+00,
-7.1024e-02, -1.2569e+00, -1.7446e+00, -1.8978e+00, -1.9663e-02,
1.5819e+00, -2.5593e+00, 4.8311e-01, -1.4362e+00, 8.9585e-01,
2.2621e-01, -6.3192e-01, 9.6575e-01],
[-3.0829e+00, -4.3344e+00, -3.8598e+00, -2.1292e+00, -2.6663e+00,
-1.8364e+00, 2.5687e-01, -6.3279e+00, -3.2069e+00, -3.2803e+00,
-1.0921e+00, -4.5912e+00, -6.8437e-01, 3.7830e-01, -3.6839e-01,
-2.0829e+00, -2.6025e+00, -4.2082e+00, -4.3396e+00, -2.9734e+00,
-2.1751e+00, -3.2557e+00, -9.7399e-01, -1.9781e+00, -1.0855e+00,
-1.8056e+00, -2.5949e+00, -4.7041e+00]],
[[ 1.7277e+00, 2.7949e+00, 1.8540e+00, 3.2673e+00, 1.2106e+00,
2.6408e+00, 2.5985e+00, 1.7675e-01, 7.6661e-01, 2.8296e+00,
1.9629e+00, 1.0371e+00, 1.0960e+00, 1.8360e+00, 2.4581e+00,
2.3240e+00, 3.4276e+00, 4.6789e-01, 2.7870e+00, 3.5721e+00,
1.4413e+00, 1.9314e-01, 5.0585e-01, 6.4904e-01, 1.0730e+00,
2.4695e+00, 6.4522e-01, 1.0604e+00],
[ 8.0561e+00, 8.7068e+00, 8.0398e+00, 1.0292e+01, 6.3139e+00,
1.0025e+01, 1.0486e+01, 5.4967e+00, 6.5935e+00, 9.6562e+00,
7.9706e+00, 8.0124e+00, 4.8594e+00, 7.4863e+00, 9.0422e+00,
8.2225e+00, 1.1548e+01, 6.4927e+00, 9.2785e+00, 1.1288e+01,
7.9983e+00, 5.3607e+00, 6.8151e+00, 5.8418e+00, 6.7265e+00,
1.0034e+01, 7.0275e+00, 6.3063e+00],
[ 1.3572e-02, -1.9507e+00, -2.8280e+00, -3.7075e-01, -3.3975e+00,
-1.0711e+00, -3.5136e-01, -3.3840e+00, -2.7964e+00, -2.3936e+00,
9.7438e-01, -3.0568e+00, 4.0147e-01, -1.8839e+00, -8.7062e-01,
1.2632e+00, -2.3820e-02, -3.5027e+00, -7.6090e-01, -8.2943e-01,
-1.7677e+00, -4.5607e+00, -3.8958e+00, -3.5944e+00, -7.7866e-01,
-7.4185e-02, -3.6162e+00, -5.5365e-01],
[-2.2992e+00, -4.0919e+00, -3.2351e+00, -1.7475e+00, -4.0110e+00,
-2.2393e+00, -2.7416e+00, -3.0424e+00, -3.3113e+00, -3.5505e+00,
-2.9581e-02, -2.9735e+00, -1.4496e+00, -3.4591e+00, -2.4393e+00,
-1.0472e+00, -1.4362e+00, -2.4217e+00, -2.8877e+00, -9.7912e-01,
-2.4756e+00, -4.1629e+00, -4.8334e+00, -4.0344e+00, -1.9015e+00,
-1.7138e+00, -2.9184e+00, -1.3584e+00],
[ 1.3143e+01, 7.6980e+00, 4.4144e+00, 9.7790e+00, 5.7849e+00,
1.3962e+01, 1.3737e+01, 9.1561e+00, 1.0076e+01, 6.7784e+00,
1.1504e+01, 1.2343e+01, 6.4229e+00, 1.0729e+01, 6.2264e+00,
1.1082e+01, 1.2218e+01, 7.7111e+00, 1.0279e+01, 1.0411e+01,
1.1958e+01, 7.6079e+00, 1.0849e+01, 5.2756e+00, 7.2323e+00,
1.5426e+01, 1.4528e+01, 1.0123e+01],
[ 7.4917e+00, 1.7766e+00, -2.4720e+00, 2.3755e+00, 6.9855e-01,
6.8079e+00, 6.0625e+00, 4.1528e+00, 4.5432e+00, -6.5834e-01,
5.4717e+00, 5.7336e+00, 2.7809e+00, 5.6617e+00, -1.0012e+00,
5.2573e+00, 3.6116e+00, 1.5208e+00, 3.8611e+00, 1.9517e+00,
5.8181e+00, 2.8174e+00, 5.1923e+00, 4.8661e-03, 1.3811e+00,
8.2654e+00, 8.8761e+00, 5.0839e+00],
[ 8.0561e+00, 8.7068e+00, 8.0398e+00, 1.0292e+01, 6.3139e+00,
1.0025e+01, 1.0486e+01, 5.4967e+00, 6.5935e+00, 9.6562e+00,
7.9706e+00, 8.0124e+00, 4.8594e+00, 7.4863e+00, 9.0422e+00,
8.2225e+00, 1.1548e+01, 6.4927e+00, 9.2785e+00, 1.1288e+01,
7.9983e+00, 5.3607e+00, 6.8151e+00, 5.8418e+00, 6.7265e+00,
1.0034e+01, 7.0275e+00, 6.3063e+00],
[ 1.7277e+00, 2.7949e+00, 1.8540e+00, 3.2673e+00, 1.2106e+00,
2.6408e+00, 2.5985e+00, 1.7675e-01, 7.6661e-01, 2.8296e+00,
1.9629e+00, 1.0371e+00, 1.0960e+00, 1.8360e+00, 2.4581e+00,
2.3240e+00, 3.4276e+00, 4.6789e-01, 2.7870e+00, 3.5721e+00,
1.4413e+00, 1.9314e-01, 5.0585e-01, 6.4904e-01, 1.0730e+00,
2.4695e+00, 6.4522e-01, 1.0604e+00]]])
Cross-attention
So, that’s it for this post. The next one will be focusing on the cross-attention, the mechanism used in Transformers to perform an attention calculus among different inputs.